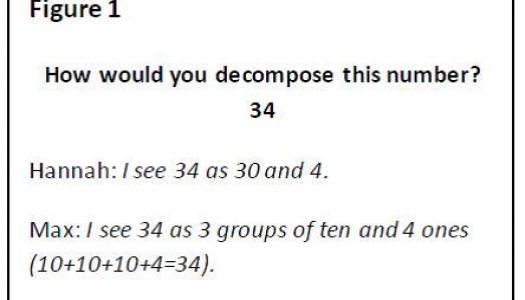Number Talks and Math Daily 3

Sherry Parrish, author of Number Talks, defines these talks as “five- to fifteen-minute classroom conversations around purposefully crafted computation problems that are solved mentally” (Parrish, 2011).

Based on Parrish’s definition, a number talk should be no longer than the length of a focus lesson. Number talks can be incorporated into the Math Daily 3 structure in a variety of ways. Here are a few suggestions to get you thinking about how you might incorporate number talks into your math routine.

• When designing your daily schedule, carve out some time to launch a number talk. Possible times include the first 15 minutes of the day, before or after lunch, and before or after specials. Be creative and intentional about carving out a designated time.
• Consider using the first focus lesson in your math block to facilitate a number talk with your students. This is a great way to help your students warm up their brains to think about math, and it can be an excellent way to elicit strategies to support the concept being taught.
• Commit to using number talks a specific number of times each week (you set the goal). Setting a goal and scheduling time will provide the consistency and structure your students rely on.

What exactly does a number talk sound like? Here is an example of a number talk while working on addition within 20.

Because it is most efficient for students to solve these problems if they learn to use strategies such as make a 10 or recognize doubles, an addition problem is created that draws out these strategies.

Teacher: We are going to warm up our brains by doing some math in our head. Remember, when we solve these problems, we don’t use any pencils or paper. I am going to show you the first problem. Once you have a solution, I want you to put your hand over your heart and sit quietly. This will let me know that you are finished solving the problem. Once I see that everyone has had a chance to solve it, I will ask for some of you to share your strategy for solving.

Write the following problem on chart paper: 3 + 7 + 4 =

Once all students (or most of them) indicate that they have a solution to the problem, move on to record all solutions.

Teacher: You quietly solved this problem and are showing me you have a solution. What is the sum of 3 + 7 + 4?
Record every sum that students have, even answers that are incorrect.

Student A: I think the sum is 14.
Record the response on chart paper.

Teacher: Does anyone think the sum is different from 14?

Student B: I think the sum is 13.
Record the response on chart paper.

Teacher: Does anyone think the sum is different from 13?
If no one else suggests a different solution, move on.

Teacher: Is there someone who will defend the solution 14?

Select someone who volunteers. Record the student’s response as he or she is sharing it. It’s okay if they make a mistake while you script their response; just correct it when they see they’ve made a mistake.

Student: I think the sum is 14 because when you add 3 and 7, you get 10. You still have the 4, so 10 and 4 make 14. It’s 14.

Teacher: If you agree that the solution is 14, give me a thumbs-up.
Look to see who agrees.

Teacher: If you used this same strategy to solve the problem, give me a thumbs-up. It’s okay if you didn’t use this strategy, because you will get a chance to share how you solved it. Did anyone use a different strategy to solve this problem? [Select someone who volunteers.] Which solution are you defending, 13 or 14?

Student: Well, I got 13 the first time I solved it, but I see my mistake and I think the answer is 14, so I am defending 14. I saw that 3 + 4 was 7. That made my problem easier, because 7 + 7 is a doubles fact. I know that 7 + 7 is 14, so I think it’s 14.

Teacher: If you agree that 14 is the solution to this problem, give me a thumbs-up.
Look to see who agrees.

Teacher: If you used this same strategy to solve the problem, give me a thumbs-up. Wow! You solved the math mentally! Making 10 and recognizing doubles are strategies that help us solve addition problems. You will have the chance to practice these strategies today during math.

As you can see from the example above, incorporating number talks encourages math conversation in the classroom and helps students think about numbers and how they fit together. You might feel out of your comfort zone when you first begin implementing number talks, but the more you try them, the easier they become

Reference:

Parrish, S. (2011). Number talks build numerical reasoning. Teaching Children Mathematics, 198–205.